-
La perspective
La perspective géométrique désigne différents procédés visant à « représenter les objets sur une surface plane de telle sorte que leur représentation coïncide avec la perception visuelle que l’on peut avoir, compte tenu de leur positions dans l’espace par rapport à l’œil de l’observateur » (Robert).

L’histoire de la perspective
Dans l'Antiquité Égyptienne (4000 à 500 av. J.-C.) les artistes ignoraient la perspective. Les personnages étaient représentés de profil, sans profondeur. Leur taille dans l'image dépendait de l'importance qu'ils avaient (symboliquement et dans ce que raconte l'image) et pas de leur éloignement.

C'est en Grèce que des philosophes et des mathématiciens établirent (de 500 à 100 av. J.-C.) que notre "image visuelle" était constituée de lignes droites partant de l'œil et formant un cône", posant ainsi les bases de la réflexion sur la perspective.
Son application dans l'art reste très intuitive, mais on sait que leslignes doivent converger pour exprimer le relief.

Le cheval de troie, dessin d'après une fresque de Pompei, 1er siècle.
La connaissance de la perspective ne progresse pas pendant le Moyen-âge, où l'aspect symbolique prédomine sur la représentation du réel.


Cependant, petit à petit, les artistes cherchaient à représenter l'espace de façon plus réaliste.


L'annonciation, Ambrogio Lorenzetti, 1344
C'est pendant la Renaissance (au XVe s. en particulier) que des artistes comme Brunelleschi, Alberti, De Vinci... cherchèrent des méthodes géométriques et sûres pour représenter en volume même les objets les plus compliqués.

L'École d'Athène, Raphaël, 1510
Ils inventent le point de fuite, point où convergent les lignes qui représentent la profondeur et que l'on appelle les fuyantes. Au début du XVIe s. apparait la notion de ligne d'horizon, ligne imaginaire qui se situe toujours devant nous, à la hauteur des yeux.
Cependant, ailleurs, comme au Japon, on développait la représentation en perspective cavalière, où les fuyantes sont parallèles entre elles, seule représentation du volume connue jusqu'aux échanges avec les occidentaux au XVIIIe siècle.

Les artistes des siècles suivant purent alors travailler en pleine connaissance de la perspective.

Les Ménines, Diego Velasquez, 1656
Au XIXe siècle, l'invention de la photographie permit la diffusion des images et permit à tous de voir et de comprendre définitivement la perspective.
Au XXe siècle, les artistes, suivant leur sensibilité, représentent la réalité ou travaillent dans l'abstraction. Ils sont libres d'utiliser ou non la perspective, ou de jouer avec elle.

Le champ de Mars, Robert Delaunay, 1911

Un autre monde, M.C. Escher
Les différents types de perspectives
perspective conique
Le procédé le plus souvent employé est la perspective conique, reprise par Filippo Brunelleschi à la Renaissance. Elle porte son nom du fait que les droites reliant l'œil de l'observateur aux contours d'un objet forment un cône. On parle aussi de projection ou perspective centrale, et encore de perspective linéaire pour désigner la même méthode. Cette technique consiste à utiliser des points de fuite pour tracer les directions et à raccourcir les distances au fur et à mesure que l’objet représenté s’éloigne de l’œil de l’observateur.

Le tableau ci-dessus date de 1476, son auteur n'est pas certain, on hésite entre Luciano Laurana, Della Francesca et Alberti. Della Francesca est l'un des tout premiers artistes à avoir représenté des tableaux construits selon les règles de la perspective linéaire, au point qu'on lui en a longtemps attribué l'invention.
Lors ce que les lignes horizontales perpendiculaires au tableau fuient toutes vers un point unique, l'ensemble constitue donc une perspective correcte (dite à un point de fuite, compte tenu de ce qu'une seule des trois directions principales présente un point de convergence fini).
Raccourcissement perspectif
Dans la conscience que nous avons du monde environnant, les objets lointains paraissent plus petits que les objets proches toutes choses égales d'ailleurs : plus un objet est lointain, plus il paraît petit.

Points et lignes de fuite
Dans le cadre de la représentation de la réalité en perspective conique, un point de fuite est un point imaginaire destiné à aider le dessinateur à construire son œuvre en perspective.
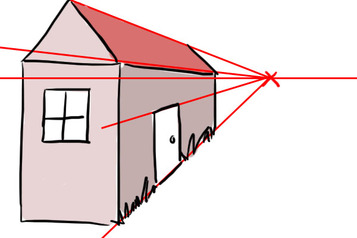
À chaque direction de l'espace est associé un point de fuite.
Il existe un point de fuite très particulier qui est celui situé dans la direction du regard. On l'appelle parfois point de fuite principal ou encore centre de la perspective. C'est le point utilisé dans les constructions dites à un point de fuite. (Les constructions dites à deux points de fuite font appel à la notion de ligne de fuite).
Différents types de perspective linéaire
Perspective à Un Point de fuite
La perspective à un point focalise une des trois séries de lignes parallèles d'un cube et les projette vers un point, le "point de fuite". Nous dirons qu'elles sont projetées vers la direction Nord. Les deux autres séries de lignes du cube restent parallèles et géométriques. Ce point de fuite peut aussi être observé lorsque votre œil se fixe sur les figures placées dans le dessin. Le point de fuite devient celui à partir duquel les cubes se déplacent dans l'espace pour montrer leur face opposée, de gauche à droite, de haut en bas.


Perspective à Deux Points
La perspective à deux points utilise deux des trois séries de lignes parallèles du cube. Elle projette une série des lignes parallèles vers le point Nord, et une deuxième série vers le point de fuite Est. Dans la perspective à deux points, la troisième série de lignes reste parallèle : dans le schéma, elles se déploient de haut en bas. Notez que les deux points utilisés ici, ceux du Nord et de l'Est, se trouvent à 90° par rapport à l'horizon. Cette "ligne d'horizon" s'appelle également la "ligne du niveau de l'œil". Il vaut mieux utiliser l'œil car lorsqu'on se trouve sous terre ou dans l'espace, il n'y a pas d'horizon mais il y a toujours le niveau de l'œil.
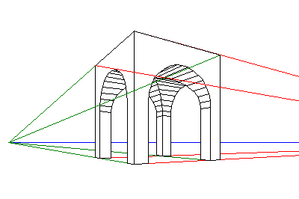

Perspective à 3 points de fuite
Ce type de perspective permet de créer des vues en plongée et en contre plongée. Comme si on regardait un immeuble soit vu d’un hélicoptère ou bien vu du sol. Dans ce cas, non seulement les lignes horizontales fuient vers un point de fuite, mais les lignes verticales aussi.
Perspective en plongée (vue de dessus)
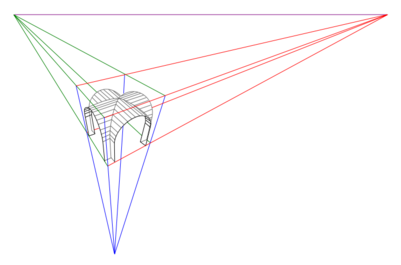

Perspective en contre plongée (vu de dessous)


On rencontre ce type de perspective énormément dans les bandes dessinées et les films d’animation japonaise qui utilisent beaucoup les mêmes plan de vu qu’au cinéma.
La perspective atmosphérique
La perspective atmosphérique est une technique principalement picturale qui consiste à marquer la profondeur de plans successifs en leur donnant progressivement (du proche au lointain) la couleur de l'atmosphère, du ciel. Elle fut redécouverte à différentes époques, les fresques de Pompéi montrent qu'elle fut utilisée dans l'antiquité.
Elle est différente du sfumato qui adoucit les contours des lointains (ou même des corps des personnages des premiers plans).

Dans le tableau La Mer de glaces de Caspar David Friedrich, les plans prennent progressivement la teinte du ciel bleu dans leur succession du proche au lointain.
Perspective cavalière
La perspective cavalière est une manière de représenter en deux dimensions des objets en volume. Cette représentation ne présente pas de point de fuite : la taille des objets ne diminue pas lorsqu'ils s'éloignent. C'est une forme particulière de perspective axonométrique, où l'on situe les points grâce à leurs coordonnées dans un repère formé de trois axes.
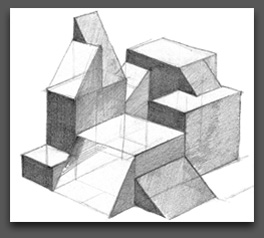
Cette perspective ne prétend pas donner l'illusion de ce qui peut être vu, mais simplement donner une information sur la notion de profondeur.
Perspective axonométrique
Cette perspective garde les mêmes principes que la cavalière avec toutefois quelques nouvelles propriétés notables.
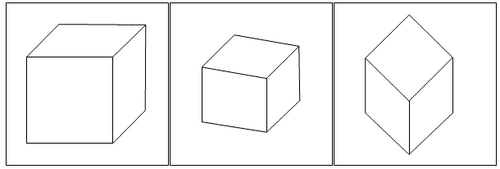
De gauche à droite : Perspective cavalière d'un cube, Perspective axonométrique d'un pavé, Perspective isométrique d'un cube
Ici, l'objet est vu par une arête. Seules les verticales en réalité restent verticales sur le dessin et parallèles entre elles. Les horizontales en réalité ne sont plus horizontales sur le dessin. Elles fuient vers deux directions opposées. Toutefois, les horizontales parallèles entre elles en réalité restent toujours parallèles entre elles sur le dessin. Lorsque l'on a trois angles de 120° la perspective est alors appelée isométrique.
Perspective isométrique
La perspective isométrique est une méthode de représentation en perspective dans laquelle les trois directions de l'espace sont représentées avec la même importance, d'où le terme.
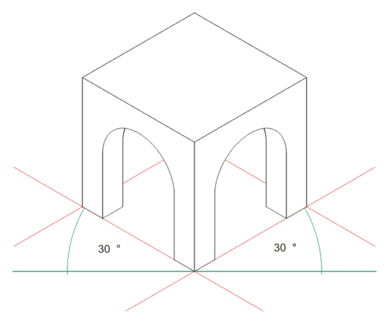
C'est un cas particulier de perspective axonométrique.
Perspective curviligne
La perspective curviligne est une technique de tracé de perspective qui veut se rapprocher de l'image rétinienne (projetée sur la sphère de l'œil).


Elle extrapole la construction de l'image jusqu'à représenter un angle de vision de 180° donc jusqu'à aller au cercle pour le cadre du dessin.

La perspective curviligne est très utilisée dans les techniques de dessin animé pour simuler la rotation d'une caméra dans un long couloir, une rue, ou un quelconque objet très long.
Afin de rendre l'effet de perspective, par exemple sur une rue où les personnages arrivent d'un côté et repartent par l'autre côté. La caméra effectue un traveling le long du décor, une feuille de papier à plat, dont le dessin utilise une perspective curviligne, simulant ainsi la rotation de la caméra dans un décor réel.
Infographie tridimensionnelle
La dénomination images tridimensionnelles est le nouveau nom donné à ce qu'on appelait dessin ou peinture en perspective depuis la Renaissance.
La synthèse d'image tridimensionnelles souvent abrégée 3D (3D pour trois dimensions : x,y,z, les trois axes qui constituent le repère orthonormé de la géométrie dans l'espace) est un ensemble de techniques notamment issues de la CAO (Conception assistée par ordinateur) qui permet la représentation d'objets en perspective sur un moniteur d'ordinateur. Elle est actuellement très utilisée en art numérique dans l'industrie du film, initiée par les studios Pixar et ILM et, depuis 1992, dans beaucoup de jeux vidéo. Il convient de ne pas faire la confusion avec les termes 3D relatifs au relief ou à la stéréoscopie.

Avant l'apparition des ordinateurs, la perspective était obtenue par des méthodes graphiques dérivées directement de la géométrie projective. Actuellement, les dessins sont calculés numériquement en partant des données numériques tridimensionnelles. Ceci permet de changer facilement le centre de projection et ses différents paramètres. En particulier, on peut calculer des séries de projections en déplaçant le point de projection et réaliser ainsi des animations.

 Tags : perspective, conique, ligne de fuite, cavalière, axonométrique, isométrique, curviligne, Infographie tridimensionnelle
Tags : perspective, conique, ligne de fuite, cavalière, axonométrique, isométrique, curviligne, Infographie tridimensionnelle
-
Commentaires
3ClaudeMardi 8 Septembre 2015 à 18:54SVP revoyez votre définition de la perspective cavalière (et l'illustration associée - voyez par exemple
http://www.pratiquemath.org/spip/local/cache-vignettes/L260xH217/persp21b-e5708.gif et
http://ajtco.free.fr/perspect/caval3.gif )
car ce n'est en aucun cas une forme particulière de perspective axonométrique. Ces 2 types de perspectives ne sont pas définies de la même façon géométriquement :
perspective cavalière : pour un cube c'est la projection OBLIQUE du cube sur un plan parallèle à une des faces du cube
perspective axonométrique : pour un cube c'est la projection ORTHOGONALE du cube sur un plan non parallèle à une des faces du cube . Selon l'orientation du plan de projection on obtient différentes perspectives axonométriques (dimétrique , trimétrique,isométrique [si le plan de projection est perpendiculaire à une diagonale intérieure du cube],...)
PERSPECTIVE CAVALIÈRE : Cette perspective est plus facile à réaliser que la perspective conique. Les fuyantes sont parallèles. Elle est couramment utilisée pour les représentations industrielles.
Tracé : Pour un cube : Projection oblique sur un plan parallèle à une des faces du cube Elle est facile à dessiner car la face avant (et toutes les faces qui lui sont parallèles) de l’objet correspond exactement à la vue géométrale associée. Il suffit ensuite de se fixer une direction de fuyantes (angle d'inclinaison alpha) ainsi qu'un coefficient réducteur k (rapport des longueurs le long des fuyantes). Le résultat obtenu donne une représentation assez correcte de la pièce. A noter que l'angle α et le coefficient k sont arbitraires,
En général: alpha = 45° et 0,5 < k < 1
Cordialement
2JeanMercredi 17 Juin 2015 à 02:191Lucie tanakaLundi 22 Avril 2013 à 10:10intéressant ;) Suivre le flux RSS des commentaires
Suivre le flux RSS des commentaires
 Ajouter un commentaire
Ajouter un commentaire
Pour les élèves en BTS et tous les curieux




Très intéressant. Merci